Research
Strongly correlated electron systems exhibit a fascinating and diverse range of physical phenomena.
Quantum many-body effects can result in collective, emergent behavior quite different from that of the
individual constituents, moving independently or treated classically. Experiment and theory advance complimentary aspects of our understanding of this
complexity. Computational studies make the link between new theoretical concepts, and experimental observations of new phenomena.
The major themes of my recent research are described below. A full list of publications can be found here.
Correlated molecular electronics
Molecular electronics offers unique scientific and technological possibilities,
which result from both the nanometer scale of the devices and their chemical complexity.
In addition to the continual drive toward miniaturization, new functionality can be
exploited when electronic components are built from single molecules because the laws
of quantum mechanics govern their basic properties.
Recent advances in the construction and characterization of molecular devices have
brought the exciting possibility of molecular electronics within close reach.
Break-junctions in nanowires can be bridged by a single molecule to complete an
external electronic circuit. A voltage bias across source and drain electrodes
drives a current through the molecular junction which is characteristic of the
structure of the bridging molecule and its contacting geometry. Intense experimental
research into the structure-function relation has demonstrated the versatility of
molecular devices and the technological utility of new design concepts.
Part of my current work involves exploring the rich new physics due to strong electronic
interactions in these molecular electronics devices.
Quantum dot nanodevices
Quantum dot devices exhibit a fascinating range of strongly-correlated electron physics.
At low temperatures in particular, Kondo physics can dramatically change the observable
transport properties. Coupled quantum dot devices offer advanced functionality due to the
interplay between orbital/geometrical effects, spin and Kondo physics. New screening
mechanisms and quantum phase transitions can be realized, and distinctive signatures
manifest in conductance.
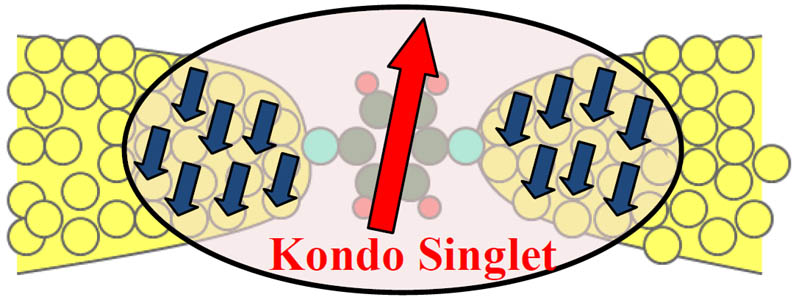
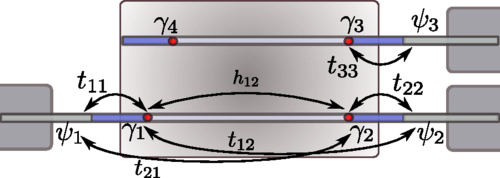
In two-dot systems, there is a complex competition between renormalized dot-lead interactions
due to the Kondo effect, and the tendency to form localized inter-dot bound states due to
direct exchange or indirect RKKY interactions:
Europhys. Lett. 76, 95 (2006)
Phys. Rev. Lett. 106, 147202 (2011)
Phys. Rev. Lett. 108, 086405 (2012)
Phys. Rev. B 85, 235127 (2012)
Phys. Rev. B 91, 235127 (2015)
Phys. Rev. B 92, 155104 (2015)
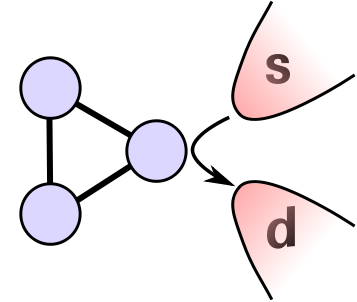
In the case of three dots, new possibilities arise -- in particular, geometrical
frustration in triangular triple dots can produce new quantum phase transitions,
accompanied by conductance switching; while in series, triple dots can realize
multi-stage Kondo screening and incipient non-Fermi liquid physics:
Phys. Rev. B 79, 085124 (2009)
Phys. Rev. B 81, 075126 (2010)
Phys. Rev. B 84, 035119 (2011)
J. Phys. Chem. B 117, 12777 (2013)
Phys. Rev. B 89, 121105(R) (2014)
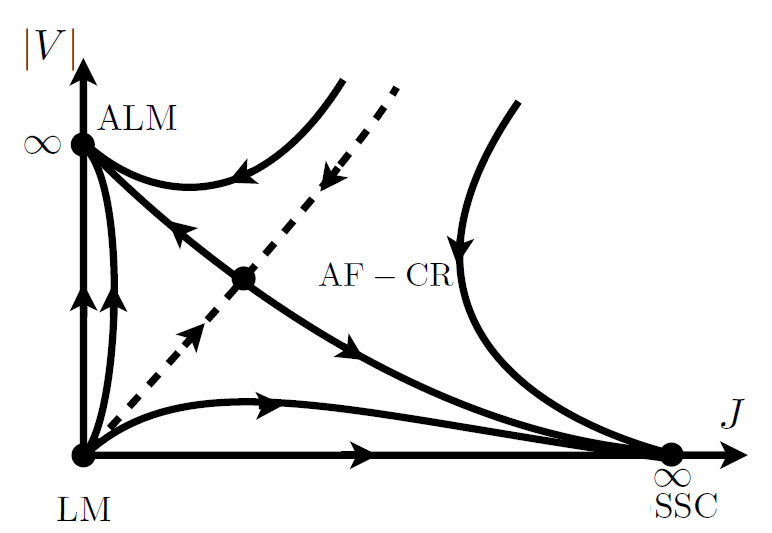
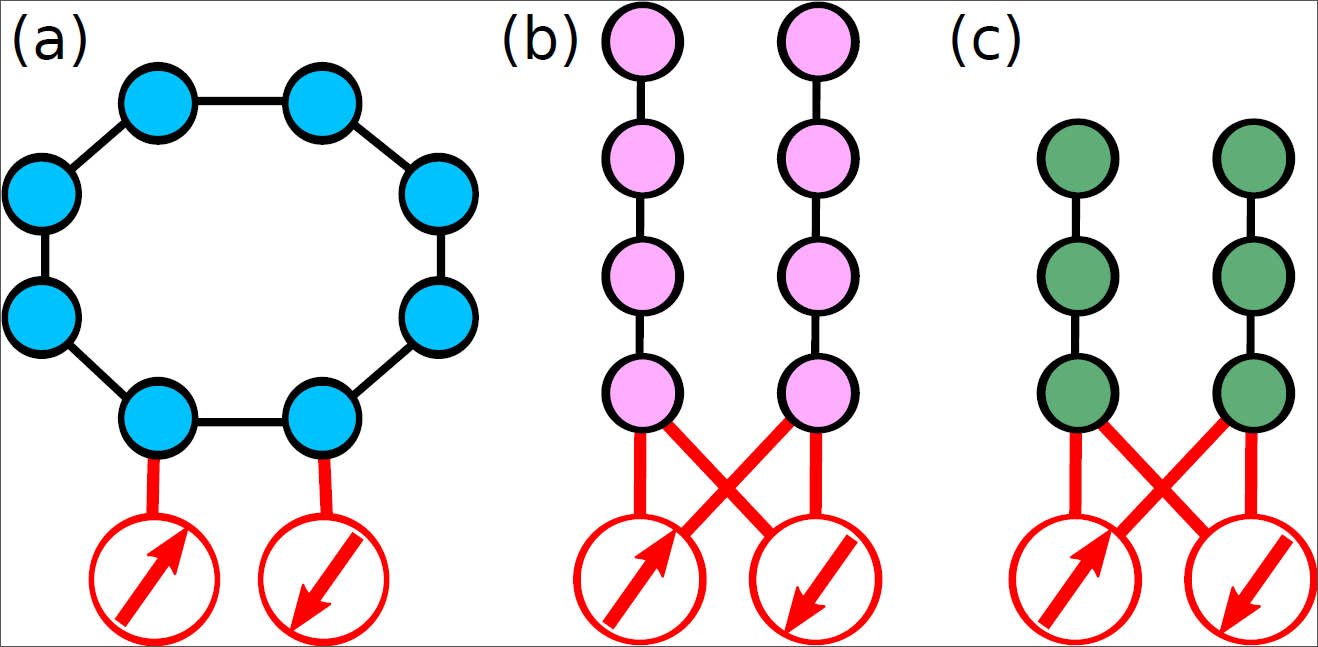
Multi-channel Kondo and critical non-Fermi liquids
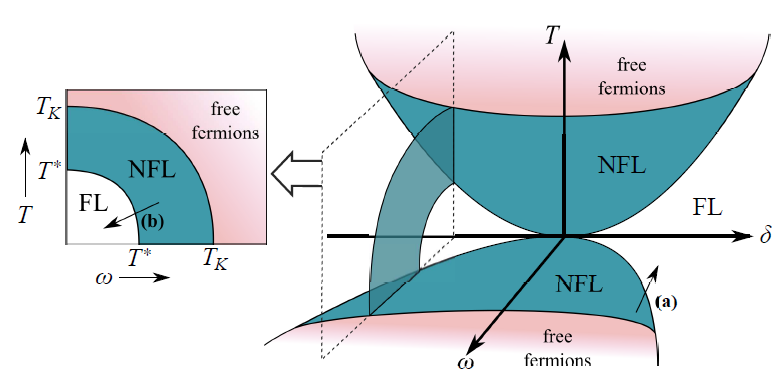
The simplest system exhibiting non-Fermi liquid (NFL) behavior
is arguably the two-channel Kondo (2CK) model, describing the frustrated
antiferromagnetic coupling of a local spin-1/2 dot
to two equivalent but independent conduction electron leads.
The resulting ground state possesses various intriguing
properties, including notably a residual entropy of
(k
B/2) ln(2) and conductance that approaches
its T=0 value as the square root of T. A different type of frustration
arises in the two-impurity Kondo (2IK) model, which features two exchange coupled
quantum dots, each also coupled to its own lead. We showed that the quantum phase
transitions and critical points of both systems are related:
Phys. Rev. Lett. 108, 086405 (2012)
Indeed, the same critical physics can be realized in all spin-S variants.
Furthermore, generalized 2CK physics arises in serial devices with a chain comprising an odd number of dots, while 2IK physics appears when there are an even number of dots:
Phys. Rev. B 84, 035119 (2011)
Quantum dot rings also show the same behaviour:
Phys. Rev. B 81, 075126 (2010)
This fascinating non-Fermi liquid physics has recently been observed experimentally in quantum dot devices:
Nature 446, 167 (2007)
Nature 526, 233 (2015)
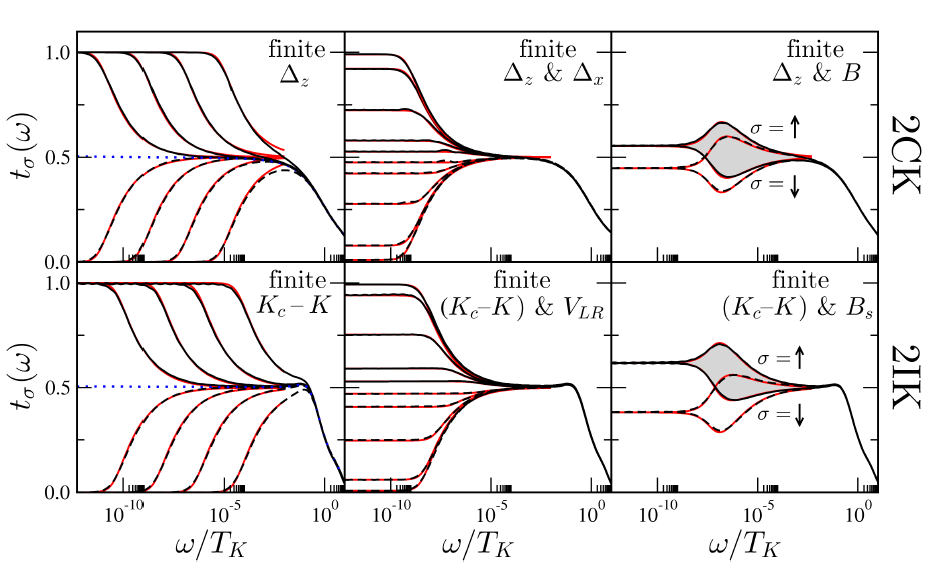
Most intriguingly, when the device is detuned away from the critical point by symmetry-breaking
perturbations (naturally present in experiments), a highly non-trivial and universal crossover
to the low-temperature Fermi liquid state is found. By exploiting a mapping to a 2d boundary
Ising model, we developed an exact theory for the crossover, including the full temperature-dependence of conductance:
Phys. Rev. Lett. 106, 147202 (2011)
Phys. Rev. B 85, 235127 (2012)
Our universal Fermi liquid crossover was very recently confirmed in state-of-the-art experiments at Stanford:
Nature 526, 237 (2015)
Real-space Kondo correlations
Most fundamental aspects of the Kondo effect are by
now very well understood, with various detailed theoretical
predictions having been confirmed directly by experiments
on impurity systems or quantum dot devices. Key insights
into the underlying physics have been provided by the
renormalization group (RG) concept, where progressive
reduction of the temperature results in
RG flow between 'fixed points' that can be easily
identified for a given model.
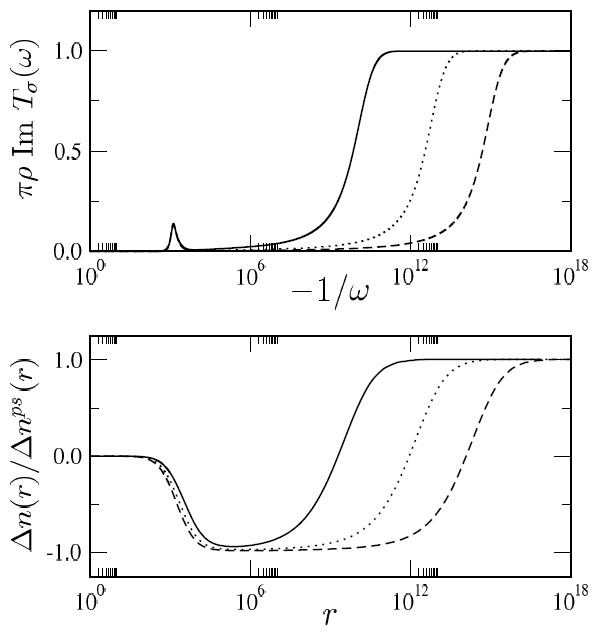
Surprisingly however, the basic physics in real-space
is still quite controversial. From theory, there is the general notion of a 'Kondo Screening Cloud' --
a macroscopic real-space region of the metallic host around a magnetic impurity, inside which electrons bind to and
dynamically screen the impurity spin. However, no real-space signatures of the Kondo Cloud have ever been
observed experimentally. In a 1d wire system hosting an impurity (realized e.g. in a carbon nanotube quantum dot),
we showed exactly and explicitly that the RG flow between fixed points can be observed in the real-space evolution of
physical quantities, such as Friedel oscillations. The impurity is rather surrounded by different fixed point clouds.
The Kondo cloud itself is really of local moment character; Kondo screening occurs on flowing to the strong coupling cloud
at larger distances. This work is published here:
Phys. Rev. B 84, 115120 (2011)
In ongoing work, we are studying real-space Kondo cloud correlations in a range of nanoscale impurity and quantum dot systems.
We are also seeking a viable proposal for the first experimental observation of the Kondo cloud.
Kondo effects in unconventional materials
We have studied unusual and exotic Kondo effects arising in a range of unconventional materials and devices, as summarized below.
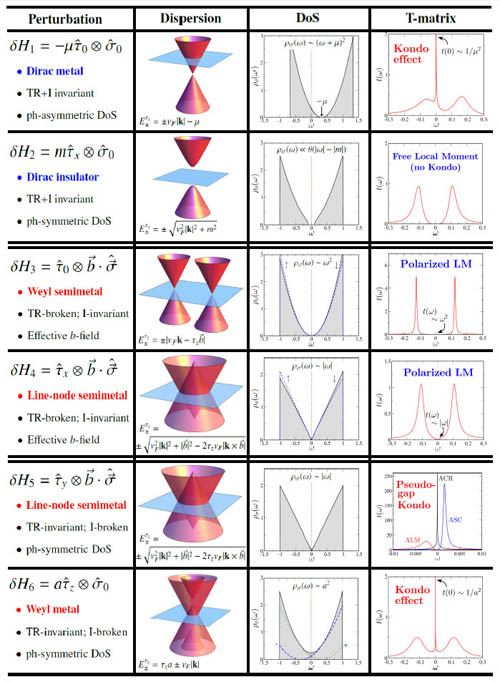
Very recently, new three-dimensional Dirac semimetal (such as Na3Bi and Cd3As2) and Weyl semimetal (such as TaAs and NbAs) systems have been discovered.
The 3d Dirac cone structure leads to a host of interesting physics. In particular, the node separation in Weyl semimetals leads to surface Fermi arcs
and the 'chiral anomaly'. We studied the effect on electronic scattering and scanning tunneling spectroscopy of magnetic impurities in these systems,
showing that different Kondo variants and pseudogap quantum phase transitions can be realized:
Phys. Rev. B 92, 121109(R) (2015)
Nanowire/superconductor heterostructures have also been the focus of much attention recently, because they host topologically-protected
fractionalized particles called Majorana fermions. One fascinating consequence of this is that real fermionic modes can be reconstructed
from spatially-separated Majoranas, producing non-local qubits which are impervious to decoherence from local perturbations.
Thus, such systems might find important application within fault-tollerant quantum computation.
However, the key role of interactions has not been fully explored. We studied the 'Topological Kondo Effect' in arising in such systems,
elucidating overscreening mechanisms and calculating numerically exactly the full conductance lineshapes expected in experiment:
Phys. Rev. B 89, 045143 (2014)
Defects in the honeycomb lattice of graphene are known to induce local moments and strong correlation effects.
Distortions due to structural reconstruction around vacancies in graphene can be formulated in terms of an effective model
consisting of a localized sigma-level hybridized with the pi-band. we analyze the rich quantum impurity physics of this system
focusing on the special role played by the unusual local density of states, which is enhanced at low energies due to potential scattering.
Depending on microscopic parameters controlled by the physical corrugations, the system can host either an exactly-screened spin-1/2 (doublet) Kondo state
or an underscreened spin-1 (triplet) Kondo state:
Phys. Rev. B 88, 075104 (2013)
The generalized powerlaw Kondo physics of defective graphene systems was analyzed in detail both analytically and numerically in:
Phys. Rev. B 88, 195119 (2013)
The metallic surface of three-dimensional topological insulators such as Bi2Te3 feature a non-trivial locking of spin and momentum.
One important consequence is that static impurities (potential defects) cannot cause backscattering, because there is no local spin-flip mechanism.
Scalar disorder therefore does not cause localization or impede current flow. By contrast, magnetic impurities,
which have a dynamic internal spin degree of freedom, do allow backscattering. Indeed, scattering is renormalized by interactions due to the Kondo effect.
But how does the peculiar structure of the topological insulator surface affect Kondo physics? What are the experimental signatures in scanning tunneling spectroscopy
and quasiparticle interference? These questions are answered here:
Phys. Rev. B 87, 075430 (2013)
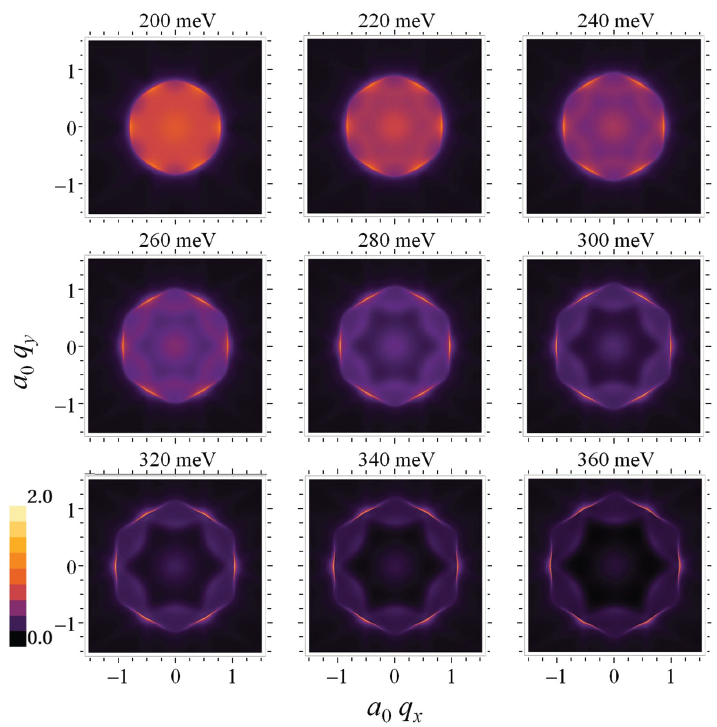
Scanning tunneling spectroscopy (STS) and Quasiparticle interference (QPI)
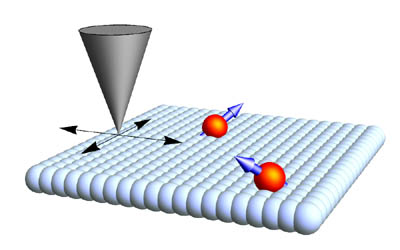
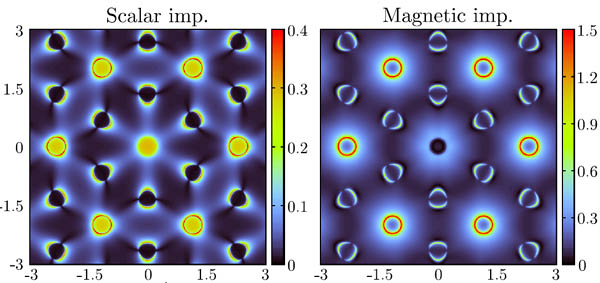
Defects or impurities in materials cause electronic scattering effects that can be locally observed experimentally using a scanning tunneling spectroscopy.
By rastering the STM across a surface, a spatial electronic density map can be built up. Its Fourier transform (FT-STS) can be interpretted in terms of quasiparticle interference (QPI).
In the case of magnetic impurities in particular, electronic scattering is characterized by non-trivial dynamics due to strong correlations and Kondo physics.
The local STS dynamics of distorted trimeric impurity clusters were studied in:
J. Phys. Chem. B 117, 12777 (2013)
The general theory of QPI due to Kondo impurities on the surface of various materials was formulated in:
Phys. Rev. B 92, 035126 (2015)
We studied the Kondo-RKKY interplay for multiple magnetic impurities on the surface of 3d host metals, calculating exactly the STS response and QPI patterns:
Phys. Rev. B 91, 235127 (2015)
QPI patterns due to Kondo impurities were also calculated on the surface of 3d topological insulators (including cubic warping effects):
Phys. Rev. B 87, 075430 (2013)
STS signatures of magnetic impurities in 3d Dirac and Weyl semimetals were discussed here:
Phys. Rev. B 92, 121109(R) (2015)
Development of numerical methods
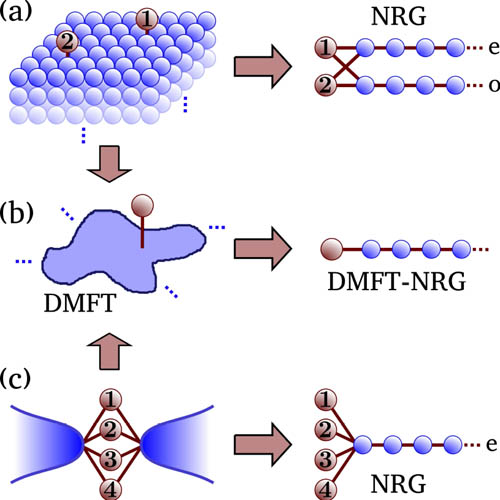
The Numerical Renormalization Group (NRG) is a powerful method for solving quantum impurity problems,
which themselves describe a diverse range of systems including interacting nanostructures, molecular electronics devices, and correlated materials within DMFT.
Thermodynamic and dynamical quantities can be obtained accurately and efficiently in the state-of-the-art implementation, on essentially any energy or temperature scale.
However, the exponential scaling of the method with the number of conduction electron channels/bands has previously prevented
application to problems involving three or more bands. This limitation was partially overcome by our breakthrough in:
Phys. Rev. B 89, 121105(R) (2014)
Our new method allows a wider range of problems to be studied exactly with NRG. The method involves mapping the multiple channels to a single interleaved Wilson chain.
This may be important for solving within DMFT multi-band lattice problems --- such as the Hubbard-Kanamori model of the open-shell transition metal oxides.
More complex problems involving many interacting degrees of freedom remain beyond reach of NRG, however.
Examples include many-impurity systems, complex molecules on surfaces and molecular electronics devices.
An appealing method to treat these systems approximately is dynamical mean field theory (DMFT), adapted to deal with inhomogenous systems. At its heart,
the method involves a local self-energy approximation, with each inequivalent site mapped to an effective impurity problem in a self-consistently-determined effective medium.
As such, the method scales linearly, rather than exponentially, with the number of interacting sites/channels. For generalized quantum impurity problems, we formulate this
'impurity-DMFT', and compare to exact NRG results for two paradigmatic models: multiple impurities on surfaces, and parallel quantum dots.
We find that impurity-DMFT works very well in some cases, but can also fail spectacularly when the Kondo effect is suppressed by inter-site correlations:
Phys. Rev. B 92, 155101 (2015)
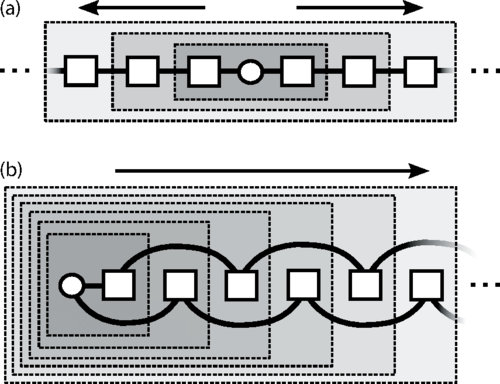
Magnetic nanostructures display a rich range of correlated electron physics, including the Kondo effect and RKKY interactions. A new feature is that of
quantum confinement: the finite size of the nanostructure leads to a discrete electronic spectrum, which cuts off low-temperature RG flow. The competition
between quantum confinement and Kondo or RKKY physics is subtle and requires sophisticated theoretical treatment. In a 1d geometry, DMRG is a powerful tool
and can be used successfully used in this context. For more general systems, another method is required. In addition, the full crossover to the thermodynamic
limit on increasing nanostructure size is an important open question. We adapted NRG to deal with these finite systems, also taking into account important Fermi
level poles which would be missed by standard logarithmic discretization:
Phys. Rev. B 92, 155104 (2015)